p-adic order
In number theory, for a given prime number p, the p-adic order or additive p-adic valuation of a number n is the highest exponent ν such that pν divides n. It is commonly abbreviated νp(n). The most important application of the p-adic order is in constructing the field of p-adic numbers. It is also applied toward various more elementary topics, such as the distinction between singly and doubly even numbers.
Properties
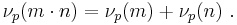
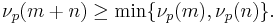 Moreover, if
Moreover, if 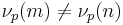 , then
, then 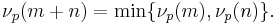
See also
References
- David S. Dummit; Richard M. Foote (2003). Abstract Algebra (3rd ed.). Wiley. ISBN 0-471-43334-9.